________________
This week, the team gathers for a post-Thanksgiving leftovers dinner and, as usual, problems ensue.
________________

Seating Arrangement
Attending the dinner are Abigail, Boris, Carla, Dashiell, Erica, Frank, Georgia, and Hari. They are sitting equally spaced around a round table, with Abigail in the northernmost seat. For each student (except Hari) you can count the number of seats you have to skip to the right of that student around the table before you come to the alphabetically next student. Those numbers are different for every student.
Where is Hari sitting?
Stuck on Fairness
When it comes time to serve the pie (which, oddly enough, is perfectly square), it turns out that only five of the teammates want to have any. Nobody wants to take any home either, so they are left with the familiar question of how to slice a square pie into five pieces of equal area. Only this time, they’re in a rush to get back home, so they want to use the smallest possible number of straight cuts. Fortunately, nobody cares how much crust he or she gets. One team member points out, “It’s impossible to cut the pie into five pieces with only two cuts, so we’ll have to use at least three.”
How do they slice the pie?
| Spread the word: | Tweet |
Solutions to week 62
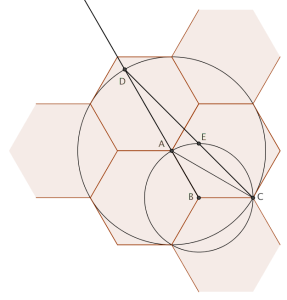
Grid Adjustment. Every good solution starts with making a diagram, like the one here. Since triangle EBC is isosceles, the plan for finding angle EBC is to determine angle ECB. To do this, note first that triangle ABC is isosceles with obtuse angle at B equal to 120°. Therefore angles ACB and BAC are 30°. Similarly, triangle DAC is isosceles with obtuse angle at A equal to the supplement of BAC, or 150°. Therefore angle DCA is 15°. But angle ECB is just the sum of ACB and DCA, so it is 45°. Finally, that means angle EBC is 90 degrees, and in fact, E turns out to be the point you need to superimpose a square grid on this hexagonal grid so that both grids share segment BC.
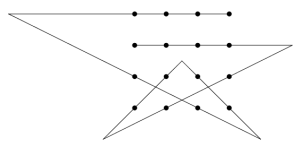
Way Outside the Box. The extra condition actually provides a bit of a hint — the first line segment must just go through four of the dots along one edge of the square. So the puzzle comes down to finding five segments that go through the remaining 3-by-4 grid. The obvious first thing to try is to build on the standard 3-by-3 solution; after all, it does “go outside the box” and hit other grid points. The problem is that solution, which is unique, also inherently involves one of the grid points lying at the junction of two of the line segments, and hence not satisfying the conditions of this problem (which require that each grid point lie on exactly one line segment). Hence, we need a completely new solution for the 3-by-4 grid. Can it be done in four lines? Any four-line solution would of course also cover one of the 3-by-3 sub-squares of points in the 3-by-4 grid, and we’ve already discarded the only 3-by-3 solution. So we know we will need at least five segments. To see if we can find such a solution, let’s try the same reduction again: if one of the five line segments goes through all four of the points along one edge of the grid, can we hit the remaining eight points with only four more segments? That now seems quite reasonable, since two points determine a line, and we can consider the eight points to be four pairs of points. If we mix up which point pairs with which, the four lines intersect each other, leading to the solution depicted below with six line segments.