Varsity Math, Week 20
Once again, the team is busy helping out in Logiton; this time, they’re not only helping the police, but also the civic planners.
Plead Insanity
It turns out that the Police Chief’s time in Non Sequitur’s headquarters (remember the Daunting Doorways problem from a few weeks ago) was not spent in vain. He was able to learn that Non Sequitur has a special punishment for bungling crimes, and that they applied it to Dana, who was very nearly caught for stealing the Trophy of Truth (Triple Jeopardy from the eighth week). This punishment drives the recipient insane. And in Logiton, everything that an insane person believes is false. But recall that criminals in Logiton always lie, which means they will only say things that directly contradict their beliefs. So for example, Dana might believe that 2+2=5 (because of being insane), and so say “2 plus 2 is not 5” (because of being a liar). Armed with this knowledge, the police round up the two remaining unidentified triplets, one of whom is Dana, and the other of whom is Chris (but it is unknown which is which). They are seated in the interrogation room on the left and right sides of a table. The police record the following testimony:
Left: I am insane.
Right: No, my sibling is not.
Left: I don’t believe what my sibling is saying!
Some important things to be aware of: Sane people in Logiton only believe true things, and Chris is either sane, or may for some other reason have gone insane since the last interrogation, in which Chris was proven to be a criminal (of a different crime). Finally, there’s no requirement that anyone in Logiton has to have a belief either way about everything. In other words, just because someone doesn’t believe a statement, doesn’t mean that person believes the opposite of that statement. That person might simply not believe either the statement or its opposite.
Which of the two triplets is Dana, the purloiner of the Trophy of Truth?
Tree-angle
The Logiton Civic Planning Commission is going to wall off one corner of the village green to create a public park in the shape of an isosceles right triangle. The highlight of this park will be four newly-planted silverbell trees. In order to thrive to maturity, each tree needs a circle of radius six meters surrounding its trunk which does not extend outside the park and which does not overlap the similar circle surrounding any other tree.
What is the minimum length of one wall of the park?
Solutions to Week 19
Staircase Surface. Since every vertical cross-section of the surface is a parabola, let’s consider the vertical cross section that contains the line of light that Jean is wondering about, and the vertical axis of the surface. Let’s put coordinates on that plane such that the vertical axis of the paraboloid is the y-axis of our coordinate system with the origin at the lowest point of the paraboloid. The line of light is a chord of the parabola in our coordinate plane which intersects the parabola at y=64 and the y-axis at (0,24). We need to know the y-coordinate of the other intersection of the chord with the parabola.
Let’s say that the horizontal distance from the first intersection point to the y-axis is d, so that its coordinates are (d,64). Then the equation of the parabola is y=(8x/d)² and the line is y=(40/d)x + 24. Therefore, when they intersect, (8x/d)² = (40/d)x + 24. Multiplying by d²/8 and bringing all terms to one side, we have 8x² – 5dx – 3d² = 0. But this factors as (x – d)(8x + 3d) = 0, so the other intersection point occurs at x = -3d/8, which leads to y=9. Hence the line of light exits the sculpture on the other side 9 units above the lowest point of the paraboloid.
The calculations would have been easier if we had assumed that the distance d was 8 units, so that the equation of the parabola was simply y=x². And as a quick-solving tip, if the problem doesn’t specify a quantity like that, you can figure that the answer must work out whatever that distance is, so go ahead and assume the nicest values for any unspecified parameters!
Word Block.
| Column number | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| A | 0 | ? | 3 | 0 | 0 |
| C | 3 | 0 | 0 | ? | ? |
| E | 0 | 1 | ? | ? | 2 |
| R | ? | 2 | ? | 0 | ? |
| T | ? | ? | 1 | 1 | 2 |
Filling in the X from the matrix with 3, the square root of the answer above, we get that the letters in each column are given by the matrix at the right. Since there are five letters in each row and five occurrences of each letter, all of the rows and columns of this matrix must add up to five.
| Column number | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| A | 0 | 2 | 3 | 0 | 0 |
| C | 3 | 0 | 0 | 2 | 0 |
| E | 0 | 1 | 0 | 2 | 2 |
| R | 1 | 2 | 1 | 0 | 1 |
| T | 1 | 0 | 1 | 1 | 2 |
That fact allows the entire matrix to be filled in fairly easily, producing the matrix on the left.
Now, to figure out how the letters are arranged in the grid, we see from the first column of the matrix that the rows are Cxxxx, Cxxxx, Cxxxx, Rxxxx, and Txxxx. Also, the other two Cs are in the fourth position, so the rows are Cxxxx, Cxxxx, Cxxxx, RxxCx, and TxxCx. Now, three of these rows have an “A” as the middle letter, so one row must be CxAxx, and the middle letter of RxxCx is either T or A, and of TxxCx is either R or A, and the other C rows have either A, T, or R as the middle letter.
At this point it is easiest just to try one of the possibilities and see if it plays out successfully. Let’s suppose that the middle As all go with the Cs, so that we have CxAxx, CxAxx, CxAxx, RxTCx, and TxRCx. The other two As are in the second position, so the last two rows would then have to be RATCE and TARCE, accounting for both of the final Es. That would mean all three other Es would be adjacent to the middle As in the raw that start with C, violating the condition that E and A are adjacent in at most one row.
Hence, we know that at least one of the middle As goes with the T or R, so the rows are CxAxx, CAxxx, Cxxxx, RxxCx, TxxCx. Let’s guess that there’s a middle A in the row that starts with R. Then, since there are no Ts in the second position, that row would have to have an E in second position and be REACT. That would use up the only allowed instance of the vowels being adjacent, so the E in CxAxx would have to be at the end, and since again there are no Ts in second position, that row would have to be CRATE.
But now the same logic shows that if there were another CxAxx row, it would also have to be CRATE, so therefore we conclude that there are two CAxxx rows. This means that the A in the TxxCx row must be in the middle, and since there are no Es left for the second column, that row must be TRACE.
That leaves just the two CAxxx rows. The only Es left now are in the fourth column, so they both must be CAxEx, and then finally, the remaining T and R in each position must alternate, for CARET and CATER.
Hence, all of the conditions are satisfied if the rows of Casey’s grid are CARET, CATER, CRATE, REACT, and TRACE — all words!
Marble Jam. Looking back to Casey’s grid, there is no letter that appears in all five different columns, but T appears in every column but the second, so the maximum number of identical letters on the diagonal is 4. That value means that if we slice the box and marbles horizontally at half the height of the marbles, the cross-section looks like the diagram on the right.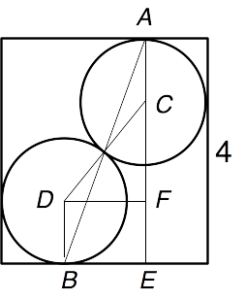
Points A and B are the two points of tangency to the walls that are 4 units apart, and hence the distance AB is 5 as specified in the problem. Drop a perpendicular from A to the side of the box that B is on, meeting that side at E, and let C and D be the centers of the two marbles. Finally, choose F on AE so that DF is parallel, and hence congruent, to BE. Then, by the Pythagorean Theorem, this common distance in three units. But then in right triangle DCF, hypotenuse DC is 2r, twice the marble radius that we are looking for, and the other leg CF is 4-2r. Therefore, by the Pythagorean theorem again, we have that 4r ² = (4-2r)² + 9 = 25 – 16r + 4r ². Canceling the r ² terms and solving, we find that r = 25/16.
Cubic Conundrum. The key to this problem is to consider the remainder when each side of the equation is divided by 9. If x and y are solutions, then those remainders must be the same. The remainder when 2405 is divided by 9 is 2, and the remainder when x³ + 2016y³ is divided by 9 is the same as the remainder when just x³ is divided by 9, because 2016 is a multiple of 9. Hence, x³ is a cubic number whose remainder when divided by 9 is 2. But taking the remainders after dividing by 9 of 1, 2, 3, 4, etc. cubed (i.e, 1, 8, 27, 64, etc.), we get 1, 8, 0, 1, 8, 0, 1, 8, 0, etc., repeating endlessly. Therefore a remainder of 2 never occurs, so there is no
Looking at equations like this in terms of their remainders when you divide by some number is called modular arithmetic. You can learn lots about different equations, and you can often use lots of different divisors. For example, in this same problem, you can also reach the conclusion that there are no solutions if you look at remainders when dividing by 7 rather than 9.
Recent Weeks
Week 19: Marble Jam & Cubic Conundrum, solution to Double Veracity
Week 18: Word Block & Double Veracity, solution to Beaver Bash
Week 16: Gonzi Scheme & New Year-amid, solution to Boxes Nest
Links to all of the puzzles and solutions are on the Complete Varsity Math page.
Come back next week for answers and more puzzles.
[asciimathsf]
