Math Monday: The ParaGons System
As mentioned recently, the DODEXcavation build was inspired by the MoMath ParaGons construction system, so let’s take a look at that. That system originated the idea of building large-scale polyhedral structures by linking polygonal panels with velcro straps. The system had its public debut at the 2016 World Science Festival, culminating in this nearly 10-foot model entitled “dodecART.”
As you can see, this structure is composed entirely of dodecahedra — regular twelve-sided solids with pentagonal faces.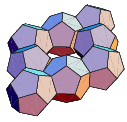
The focus on dodecahedra began with this observation that it is possible to arrange eight dodecahedra face-to-face to form a closed loop in the shape of a rhombus. Further investigation revealed that the rhombus, as measured from the centers of the four dodecahedra on the corners, is a golden rhombus, in which the ratio of the the long to short diagonal is the golden ratio, (1+√5)/2.
That fact in turn suggested that it might be possible, by connecting further dodecahedra, to create any of the structures shown near the bottom of the golden rhombus page, such as the lovely rhombic triacontahedron shown at left. And as the first picture shows, that possibility turns out to be true: the centers of the red and blue dodecahedra are precisely at the vertices of a rhombic dodecahedron.
Could one build any of those structures? What else might we build? The answer, as might not surprise you, again lies with Zometool.
Anything you can build using only red lines of Zometool can be constructed by gluing dodecahedra face-to-face. For example, you might make this pentagonal crown (actually one quarter of a rhombic hexecontahedron). Why does this work out? The pentagonal faces of the Zometool hub are at exactly the same angles as the faces of a regular dodecahedron, and opposite faces of a dodecahedron have the same 36-degree twist with respect to each other as the two ends of a red Zometool strut. That probably sounds very reminiscent of what we said about icosahedra in a recent column. But that’s no accident — because the icosahedron and dodecahedron are dual polyhedra, the Zometool hub is also a cantellated dodecahedron.
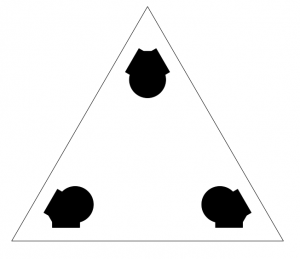
The ParaGons system is not meant to be limited to pentagons. For example, here is a cut file for a square ParaGon, and a pattern for a scaled-down triangle (the ParaGon side length is 20 cm) in the DODEXcavation style which would be compatible with ParaGons. Note the smaller scale creates a need to merge the holes nearest each vertex (since unfortunately you can’t scale down your fingers).
We close this series on large-scale polyhedral constructions with some pictures of ParaGons builds in action, and the latest construction, a rhombic icosahedron at the Google Geek Street Fair.
