Math Monday: DODEXcavation
 So what’s the purpose of this model that we’ve been struggling to build for the past few weeks? Well, it began when a friend asked for a corporate group-building event at Andrew Davidson & Co. in New York. The goal was to have a large geometric structure which could be assembled from modules, each built by a different team. Inspired by the success and the design of MoMath’s ParaGons construction system (which will be the subject of its own upcoming column), it seemed that a large-scale polyhedral construction might fit the purpose nicely. That’s when the explorations recounted in the last few columns began.
So what’s the purpose of this model that we’ve been struggling to build for the past few weeks? Well, it began when a friend asked for a corporate group-building event at Andrew Davidson & Co. in New York. The goal was to have a large geometric structure which could be assembled from modules, each built by a different team. Inspired by the success and the design of MoMath’s ParaGons construction system (which will be the subject of its own upcoming column), it seemed that a large-scale polyhedral construction might fit the purpose nicely. That’s when the explorations recounted in the last few columns began.
Once the model was complete and the excavated dodecahedron structure was selected for the build, the project was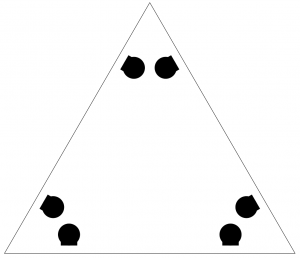 dubbed “DODEXcavation,” and production began. The target height for the completed project was between nine and ten feet, so the triangles needed to be scaled up to 36 cm on a side. Next, I had to generate a pattern for the individual triangular tiles, like so (click on the image for a PDF of the pattern file; the small red square is for scale, it should be one centimeter on a side). Similarly to the way ParaGons are used, participants would loop velcro strapping through the holes near the edges of the tiles (shown in black), binding the tiles together along an edge. I worked with Precision Waterjet & Laser in Placentia, CA to have almost 1,000 copies of this pattern cut from three colors of corrugated plastic: yellow for the octahedra, blue for the icosahedra at the center of each face, and green for the icosahedra at each vertex.
dubbed “DODEXcavation,” and production began. The target height for the completed project was between nine and ten feet, so the triangles needed to be scaled up to 36 cm on a side. Next, I had to generate a pattern for the individual triangular tiles, like so (click on the image for a PDF of the pattern file; the small red square is for scale, it should be one centimeter on a side). Similarly to the way ParaGons are used, participants would loop velcro strapping through the holes near the edges of the tiles (shown in black), binding the tiles together along an edge. I worked with Precision Waterjet & Laser in Placentia, CA to have almost 1,000 copies of this pattern cut from three colors of corrugated plastic: yellow for the octahedra, blue for the icosahedra at the center of each face, and green for the icosahedra at each vertex.
As a test of the pieces, I made up this model of an excavated dodecahedron, showing schematically what we would be building.

Finally the day of the build arrived, and the participants split up into teams and began to unwrap their individual packets of materials. We had settled on twelve teams, so that each team would be constructing one of the blue icosahedra, and either one or two of the green icosahedra (with holes to connect to other modules). In fact, it turns out that the full excavated dodecahedron can be broken up into four copies of each of the following three pieces (I’ll let you figure out how on your own).
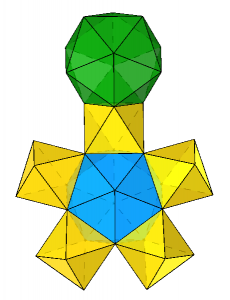
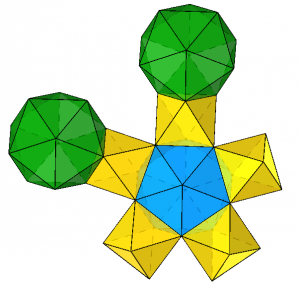
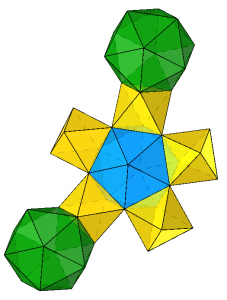
As the teams got into the project, you could see some of the familiar structures from the prototyping process take shape, only now about ten times as large.




Of course, there were some blind alleys but these were mostly corrected pretty easily. (The issue in the picture above was that the pentagonal cap was connected to five square pyramids, not octahedra.)
(The issue in the picture above was that the pentagonal cap was connected to five square pyramids, not octahedra.)
Here’s a team with their fully complete module. 
Maneuvering five-foot-long modules into position to connect them to each other proved challenging.


And here’s the essentially complete structure.

As you can see, it’s not quite ten feet tall, as time limitations prevented the completion of all necessary connections, leading to some internal buckling of the structure. But a good time was had by all, and you can clearly see the five-fold connectedness of the excavated dodecahedral structure. If you’d like to try building some polyhedra, you can cut copies of the pattern (scaled down, presumably) out of stiff paper and connect them with twist ties (for example) — send a picture to mondays@momath.org if you do!

