The Math of Pythagorize the Flatiron
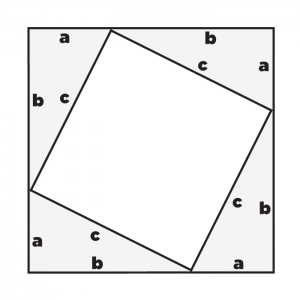
To see how these triangles prove the Pythagorean theorem, we calculate the area of the large square in two different ways.
First, we see that the length of the side of this square is (a + b), so the area of the whole square is
(a + b)2 = a2 + 2ab + b2.
Now we compute the area of the same square by noticing that this square is made up of a smaller square of side length c and four right triangles of height a and width b. So the area of the larger square equals the area of the smaller square plus the area of the four triangles. This smaller square has area equal to c2 and each triangle has area equal to 1⁄2(ab). Adding the areas we get a total of c2 + 2ab.
Now let’s compare the two computations. On one hand, the area of the larger square is a2 + 2ab + b2 and on the other hand the area of this same square is c2 + 2ab. So it must be that a2 + 2ab + b2 = c2 + 2ab. Subtracting 2ab from both sides of this equation we get a2 + b2 = c2. In other words, the sum of the squares of the lengths of the legs of a right triangle is equal to the square of the length of its hypotenuse.