Math Monday: Those Circles are GREAT!
by Glen Whitney
Namely, that medium is the “CD Ball” by Gordon Stallings. The simplest of these is the three-CD version:
The four-CD version reproduces the hula hoop arrangement from the earlier column linked to above, in which the points of intersection lie at the vertices of a cuboctahedron, one of the 13 Archimedean solids:
Before we show you the spoiler, here’s an interesting arrangement of six great circles which does not solve the problem above. It’s “Orbital Connection” by the sculptor Hera, installed in a courtyard of New York’s Governor Smith Housing Authority complex:
In this case, the great circles appear to lie in the planes perpendicular to the six two-fold axes of symmetry of a cube. And now for Gordon’s six-CD ball:
In this construction, the points of intersection lie at the vertices of an icosidodecahedron, another Archimedean solid, which guarantees that the distances between them are all identical.
But the great circle fun does not stop there: here’s a seven-CD construction based on the three-fold and four-fold axes of symmetry of a cube:
And I will leave you with a challenge. Construct a physical model of the following highly symmetric arrangement of 15 great circles on a sphere (in any medium you choose), submitted by Sandor Kabai to the Wolfram Demonstrations Project: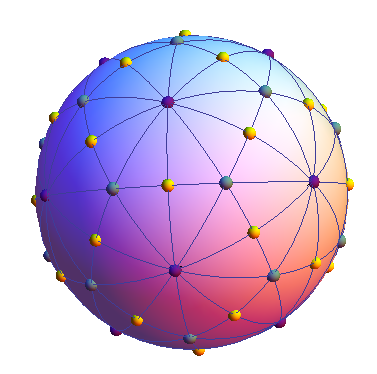
If you build one (or any other interesting great circle composition), please send a photo or two to mondays@momath.org. We love to see what you’re up to.
This article first appeared on Make: Online, July 23, 2012.
