Math Monday: Grocery Geometry Revisited
by Glen Whitney
First, the equilateral triangular prismatic packaging of a familiar chocolate candy provides lots of scope for geometrical construction. In that vein, we offer the following recipe:
Tetrablerone
Ingredients: 12 Toblerone bars in original packaging (three each of four flavors for best results)
8 rubber bands
Serves: thousands, hopefully
Mix all ingredients as indicated in the following picture. Note that this structure takes advantage of the following two pinwheel-like arrangements of triangular prisms around one point in which each prism lies flat against its two nearest neighbors, consisting of three and four prisms respectively. Note that each of these pinwheels by itself can be held together with a single rubber band around its equator.
Note that this structure takes advantage of the following two pinwheel-like arrangements of triangular prisms around one point in which each prism lies flat against its two nearest neighbors, consisting of three and four prisms respectively. Note that each of these pinwheels by itself can be held together with a single rubber band around its equator. There are eight three-bar pinwheels and six four-bar pinwheels in the completed Tetrablerone, although of course each bar participates in several of these pinwheels. How can you quickly figure out how many pinwheels each bar appears in?
There are eight three-bar pinwheels and six four-bar pinwheels in the completed Tetrablerone, although of course each bar participates in several of these pinwheels. How can you quickly figure out how many pinwheels each bar appears in?
If you can find a fifth flavor of Toblerone, you can make a lovely five-bar pinwheel as well: Note that in each of these pinwheels, the supporting rubber band becomes a regular triangle, square, or pentagon parallel to the table, respectively. If you are looking for an interesting challenge, figure out the side lengths of each of these polygons, assuming the original triangular prisms have cross-section that is an equilateral triangle of side length 1. Is there a larger structure that incorporates several five-bar pinwheels? If you make something along those lines, send in a picture!
Note that in each of these pinwheels, the supporting rubber band becomes a regular triangle, square, or pentagon parallel to the table, respectively. If you are looking for an interesting challenge, figure out the side lengths of each of these polygons, assuming the original triangular prisms have cross-section that is an equilateral triangle of side length 1. Is there a larger structure that incorporates several five-bar pinwheels? If you make something along those lines, send in a picture!
Speaking of sending things in, here’s a reader submission of Sierpinski Gumdrops: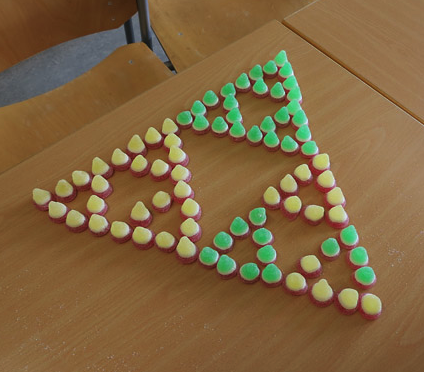 You can find more of Geneviève Harles’s food fractals here and here. Keep the lovely work coming!
You can find more of Geneviève Harles’s food fractals here and here. Keep the lovely work coming!
This article first appeared on Make: Online, October 22, 2012.

