Varsity Math, Week 9
Heading toward the Fall break, it’s Game Day for the Varsity Math team. But even when they’re at play, the team can’t help but find puzzles to chew on. At least there’s a break from the relay…
Minipixel | Junior Varsity
One of the favorite pastimes of the team is pixel puzzlers. In this type of puzzle, every row and column of a square grid is labeled with a sequence of numbers indicating the lengths of all of the separate runs of adjacent black pixels to be filled in within that row or column. (See the example diagram.) The goal is to deduce which pixels are black and re-create the unknown picture.
Assuming every row and column is labeled with a single non-zero number less than the size of the grid, what is the smallest number of black pixels a pixel puzzler can have and be uniquely solvable?
Stick Tac Toe | Varsity
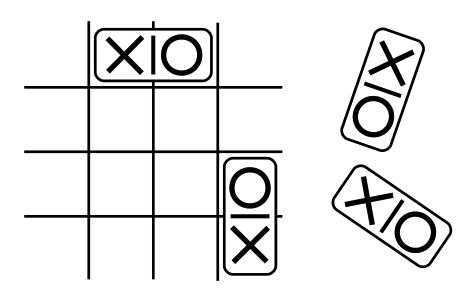
The team has invented a new version of an old favorite. In Stick Tac Toe, the Xs and Os are stuck together: one of each on the two spaces of a domino. The team members play on a four-by-four board, with four dominos each. The first player plays “X”, but each turn consists of placing a domino to cover two empty spaces of the board, so both an “X” and an “O” will be placed on the board, in positions that are horizontally or vertically adjacent. The goal remains the same: to get three of your marks in a row, horizontally, vertically, or diagonally. Unlike Tic Tac Toe, this game is not destined to be a tie—the first player can force a win. There’s one unusual situation that can come up in Stick Tac Toe: if a player lays down a domino that simultaneously completes both a row of three “X”s and three “O”s, she or he is still considered to have won. On the other hand, if a player completes a row of the opponent’s marks without making one of his or her own, the opponent wins.
Assuming optimum play from both players, what is the maximum number of dominos the second player can guarantee to be able to place on the board before losing? (Note that the notion of optimum play includes the mandate for each player to try to win as quickly as possible and to survive for as many turns as possible in a losing game.)
Solutions to Week 8
Geometric Addition. The common ratio will show up after the relay is done.
Triple Jeopardy. Let’s start by giving the Left suspect the benefit of the doubt. If Left is completely innocent so that the first statement is true, then the Middle statement must also be true. But now there’s a problem; there are only two ways the Middle statement could be true, and neither works. If Dana committed an unrelated crime, that we have both Chris and Dana as liars, but in this scenario Left and Middle are both completely innocent, and there are only three triplets. If the third sibling is Elliot, then Chris who stole the trophy is one of the first two, but again in this scenario the first two are completely innocent. So it doesn’t work for Left’s statement to be true. So we know that Left has committed some crime, and therefore that either Chris did not steal the Trophy, or the Middle sibling committed some crime.
Could the Middle sibling be innocent? Based on just the first three statements, yes; that would make Right’s first statement true, so Right would be completely innocent, and based on what the Middle sibling said, either the first sibling is named Dana and committed some unrelated crime, or the third sibling is named Elliot. The important thing is that in either case, for the Middle sibling to be innocent, both Middle and Right have to be innocent and one of them must be named Elliot.
That means that Middle blows the guise of innocence by accusing Elliot. If that accusation were correct, then Elliott would be guilty, but in the scenario in which Middle is telling the truth, Elliot is innocent.
Hence, Middle is lying, and guilty of something. Hence Dana did not commit an unrelated crime, and Right is not named Elliot.
Looking back at Right’s first statement, we now know it to be false, so Right has also committed some crime. Since all three triplets are guilty of something, and Dana did not commit an unrelated crime, we conclude that Dana stole the Trophy of Truth.
Finally, can we figure out the names of any of the triplets? Right is not named Elliot, and since Right claims that Elliott tried to finger Chris, which must be false, Left cannot be named Elliott, since Left did try to finger Chris. So the Middle triplet is named Elliot.
Unfortunately, all of the statements are now properly inconsistent with the facts (given that all three triplets are liars), and so there is not enough information to determine whether Left or Right is named Dana/stole the Trophy. Hopefully the Logiton police will be getting some more leads in this case at some point…
Previous Weeks
Week 8: Triple Jeopardy & Geometric Addition, solutions to Week 7
Week 7: Hex Truss & Windows on the World, solutions to Week 6
Week 6: Cross Training & Sesquicycle, solutions to Week 5 and Relay 1
Week 5: Laborious Lockup & Prime Event, solutions to Week 4
Week 4: Unsustainable Agriculture & Save the Camel, solutions to Week 3
Week 3: Deranged Assistant & Rush Job, solutions to Week 2
Week 2: Carambola Orchard & Farm Roundup, solutions to Week 1
Week 1: Instant Interrogation & Urn Respect
Find more puzzles at varsity.momath.org.