Varsity Math, Week 13
The new three-week relay wraps up today, with what Coach Newton terms “a visit to the Platonic world of geometry (with maybe a little trigonometry thrown in).”
Try Angles
Isosceles triangle △`ABC` has shortest side `AC`. Points `D` and `E` are on sides `AB` and `BC`, respectively. The degree measure of angle `/_EAC` is equal to the last two digits of the answer to Tee Party from two weeks ago. 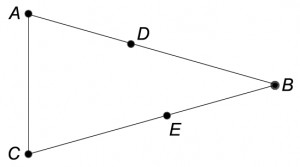 The degree measures of angles `/_DCB` and `/_EAB`, respectively, are ten times the first and second digits of the answer to Slingshot Grid from last week. Note that the diagram is not necessarily to scale.
The degree measures of angles `/_DCB` and `/_EAB`, respectively, are ten times the first and second digits of the answer to Slingshot Grid from last week. Note that the diagram is not necessarily to scale.
What is the degree measure of angle `/_DEA` ?
Great Lengths
Points F, G and H are all on a line in the order listed, with distance FG = GH. Moreover, this common distance is an integer. Point J is on the same line, on the other side of F from G. Distance JF is also an integer. If you make a triangle with side lengths equal to JF, JG and JH, one angle of that triangle is twice another angle of that same triangle.
What is the smallest possible length JF?
Solutions to Week 12
Daunting Doorways. Let’s dive in by assuming that the sign on Door 1 is true. Our goal is to see if there’s an assignment of traps to doors which is consistent with that assumption. In this scenario, Door 1 would then have a trap, Door 5’s sign would have to be false, so Door 4 would have to have a trap, and Door 2 would have to be safe (so that the sign on Door 1 could be true). If you also assume that Door 3 is safe, then the sign on Door 4 would have to be true and so Door 5 would have to have a trap. Double-check that now all of the signs are consistent with the rules. Therefore, one possible scenario has traps on Doors 1, 4 and 5, so the Chief cannot try to escape through any of those doors.
What about Door 2? Is there a consistent scenario in which that door has a trap? In fact, if it’s the only trapped door, then you can see that its sign is true as required, and none of the other signs matter (since those doors are safe in this scenario, their signs can be either true or false). So the Chief cannot be sure that Door 2 is safe.
Therefore, by process of elimination, the Chief should escape through Door 3.
Anything bothering you? That Non Sequitur sounds like a pretty nasty organization. How do we know Door 3 is really safe, beyond simply being the only option left? In other words, how do we know the problem even has a solution?
Let’s probe a little deeper and find out. We want to figure out if there is any self-consistent way to assign a trap to Door 3. There are two main cases: either both adjacent doors (2 and 4) are trapped, in which case the sign on Door 3 is false, or at least one is safe, in which case the sign on Door 3 is true.
In the first case, there are an odd number of traps, so either all five doors have traps or just Doors 2 through 4 have traps. But we can’t have all five doors have traps, because then all the signs would be false, but the sign on Door 2 is true in such a case. And it can’t be just Doors 2 through 4, because then the sign on Door 4 would have to be true, but it’s not in that case. So we conclude that if Door 3 has a trap, then its sign must be true and Door 2 or Door 4 (or both) is safe.
Now we need to consider the possibilities for an even number of doors with traps. Either all of the doors have traps except for 2 or 4, or Door 3 and just one other door have traps. Let’s eliminate the cases with four booby-trapped doors first. If just Door 2 were safe, then the sign on Door 4 would have to be false, but it’s actually true in that case. If just Door 4 were safe, then Door 2 would have to be false, but it turns out to be true then.
That leaves just the possibilities with Door 3 and one other door hiding traps. Then both of the doors with traps would have to have true inscriptions. We already know from above that if Door 1’s sign is true, then Door 4 must have a trap, so it can’t be just 1 and 3 with traps. If just Doors 2 and 3 had traps, the sign on Door 2 would be false. If it were Doors 3 and 4, then Door 4 would be false. And finally, if just Doors 3 and 5 had traps, then Door 5 would be false.
So in fact, as implied by the statement of the problem, there is a door, namely Door 3, which cannot have a trap in any scenario allowed by the rules. Go, Chief, and go, team!
Recent Weeks
Week 12: Daunting Doorways & Slingshot Grid, solution to Design Data
Week 10: Mile High Stretch & Self-Sequential Reference, solutions to Minipixel and Stick Tac Toe
Week 9: Minipixel & Stick Tac Toe, solution to Triple Jeopardy
Links to all of the puzzles and solutions are on the Complete Varsity Math page.
Come back next week for answers and more puzzles.