________________
________________

World Turns
Coach Newton reminds the team that the Earth is constantly rotating about an axis that connects the North and South Poles. “Umm, yeah,” responds the team. “Ask us something we don’t know.”
Rounded to the nearest quarter-turn, how many rotations on its axis does the Earth make per year, averaged over many years?
Water Slide
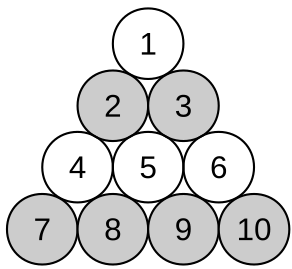
 Coach Newton sets up ten glasses arranged in a triangle as shown, with the glasses numbered 2, 3, 7, 8, 9, and 10 full of water and the others empty. He challenges the team to rearrange the glasses into the second configuration shown, with full glasses at positions B, C, E, G, H, and I, and in which the triangle points in the opposite direction.
Coach Newton sets up ten glasses arranged in a triangle as shown, with the glasses numbered 2, 3, 7, 8, 9, and 10 full of water and the others empty. He challenges the team to rearrange the glasses into the second configuration shown, with full glasses at positions B, C, E, G, H, and I, and in which the triangle points in the opposite direction.
What is the smallest number of glasses the students can move to perform Coach Newton’s challenge?
| Spread the word: | Tweet |
Solutions to week 88
Soccer or Math? Since Duke is tied exactly at one right angle of the square, and the square won’t fit through the goalposts, Duke is always at the vertex of a right triangle whose two other vertices are the goalposts. In fact, Duke can be at any point which makes a right triangle with the two goalposts, and the goal line will always be the hypotenuse of the right triangle (since Duke is tied up at the right angle). The collection of all of the vertices of right triangles on the same side of a line segment that have that line segment as hypotenuse is a semicircle whose diameter is that line segment (this is covered in many introductory geometry classes; for a quick calculation showing that it must be so, see the box below). So we are just looking for half the perimeter of the circle whose diameter is the 7.32-meter long goal line. That’s π×7.32/2, which turns out to be very close to eleven and a half. So rounding as requested, the desired length is eleven meters.
Belt, Suspenders, and Braces.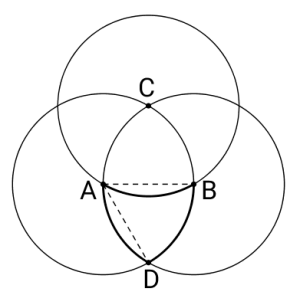 In the diagram, the points A, B, and C represent the three trees, and the circles represent the regions in which Duke could roam if he were only chained to that one tree. So with all three chains in place, Duke can only reach points in the intersection of all three circles, namely that shape in the center that looks like a triangle with curvy sides. (It’s actually called a Reuleaux triangle.) If the chain to tree C breaks, let’s say, then Duke can reach any point in the intersection of the circles centered at A and B, which is a sort of pointy oval reaching from C down to D. So the additional area he can reach when one chain breaks is the region outlined in a heavier stroke. That might seem daunting to calculate the area of, but notice that if you cut off the slice indicated by the dashed line, it just fits into the top depression in the shape as indicated. Therefore, the extra area is simply one sixth of the entire circle centered at A, or 36π/6 = 6π square meters.
In the diagram, the points A, B, and C represent the three trees, and the circles represent the regions in which Duke could roam if he were only chained to that one tree. So with all three chains in place, Duke can only reach points in the intersection of all three circles, namely that shape in the center that looks like a triangle with curvy sides. (It’s actually called a Reuleaux triangle.) If the chain to tree C breaks, let’s say, then Duke can reach any point in the intersection of the circles centered at A and B, which is a sort of pointy oval reaching from C down to D. So the additional area he can reach when one chain breaks is the region outlined in a heavier stroke. That might seem daunting to calculate the area of, but notice that if you cut off the slice indicated by the dashed line, it just fits into the top depression in the shape as indicated. Therefore, the extra area is simply one sixth of the entire circle centered at A, or 36π/6 = 6π square meters.
 Extra from Coco-Not last week: If everyone plays by the optimal strategy, then you know what color they will choose based on what’s been drawn; basically they draw alternate colors until a coconut turns up, and then everyone chooses the same color of chocolate once a coconut has shown up, until it is exhausted. That means we can create the tree diagram as shown; each node represents a person choosing a chocolate and the left-hand branch represents choosing coconut and the right-hand branch represents choosing non-coconut. Note that we do not have to follow up most of the left branches, because Coach Taylor is safe if any coconut is chosen before her, unless her grandmother (who takes the first pick) got it (then the intervening group of five people take all the rest of that color). So the branching probabilities are based on what color each person chooses under the optimal strategy. The two nodes in which Coach Taylor gets a coconut are colored in red. The aggregate probability of the red nodes is (1/6)(1/6) + (5/6)(5/6)(4/5)(4/5)(3/4)(3/4)(1/3) = 1/36 + 1/12 = 1/9, nearly twice the chance of getting coconut than if the other relatives were choosing at random.
Extra from Coco-Not last week: If everyone plays by the optimal strategy, then you know what color they will choose based on what’s been drawn; basically they draw alternate colors until a coconut turns up, and then everyone chooses the same color of chocolate once a coconut has shown up, until it is exhausted. That means we can create the tree diagram as shown; each node represents a person choosing a chocolate and the left-hand branch represents choosing coconut and the right-hand branch represents choosing non-coconut. Note that we do not have to follow up most of the left branches, because Coach Taylor is safe if any coconut is chosen before her, unless her grandmother (who takes the first pick) got it (then the intervening group of five people take all the rest of that color). So the branching probabilities are based on what color each person chooses under the optimal strategy. The two nodes in which Coach Taylor gets a coconut are colored in red. The aggregate probability of the red nodes is (1/6)(1/6) + (5/6)(5/6)(4/5)(4/5)(3/4)(3/4)(1/3) = 1/36 + 1/12 = 1/9, nearly twice the chance of getting coconut than if the other relatives were choosing at random.
Recent Weeks
Week 88: Soccer or Math? & Belt, Suspenders, and Braces, solutions to Queen Bee & Coco-Not
Week 87: Queen Bee & Coco-Not, solutions to Uneven Odds & Stable Selection
Week 86: Uneven Odds & Stable Selection, solutions to Peri-area? & Hypotenuse Partition
Week 85: Peri-area? & Hypotenuse Partition, solutions to Potato Puzzle & Cucina Combinations
Week 84: Potato Puzzle & Cucina Combinations, solutions to Sour Lemons & One Liner
Links to all of the puzzles and solutions are on the Complete Varsity Math page.
Come back next week for answers and more puzzles.