Recent Groundbreaking Discoveries in Mathematics

The Hat and the Spectre

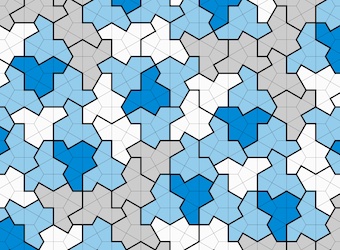
In tiling the plane, the Hat mixed unreflected and reflected tiles, leaving open the question of whether a single shape could tile aperiodically using translations and rotations alone.  This question was answered with the exciting discovery of the Spectre, an aperiodic monotile that is “chiral,” meaning that reflected copies of the tile are not needed to form a tiling and no tiling with unreflected copies has a repeating pattern.

The Hat in the Press

The Einstein Mad Hat Competitions

To celebrate the recent discovery of the Hat and Spectre tiles, which tessellate the plane but only in a non-repeating way, the National Museum of Mathematics and the United Kingdom Mathematics Trust organized The Einstein Mad Hat Competitions, seeking creative renditions of the Hat and Spectre tiles.

Check out the winners of the Einstein Mad Hat Awards.

_____________

Learn about the first discovery: the Hat

Presenting “the Hat,” a newly discovered (and first-ever!) shape that can tile the plane endlessly but only without ever quite repeating the pattern.
 
An Aperiodic Monotile
By David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss
Read the groundbreaking paper about “the Hat,” a new discovery in mathematics.

Hear the story

A Hat for Einstein
(Recorded event from Sunday, March 25)
Join Craig S. Kaplan and Chaim Goodman-Strauss who, along with their co-authors David Smith and Joseph Samuel Myers, wrote the groundbreaking paper about the Hat.  They will discuss how they discovered this aperiodic monotile and how it impacts modern mathematics.  Watch the video.

Meet the Authors
(Recorded event from Wednesday, March 29)
Join all four authors of the groundbreaking paper, David Smith, Joseph Samuel Myers, Craig Kaplan, and Chaim Goodman-Strauss, as they discuss their exciting mathematical discovery of the Hat, the first-ever shape that can tile the plane endlessly but only without ever quite repeating the pattern.  Have your questions answered — or just enjoy the lively discussion — at this interactive Q&A session!  Watch the video.

Announcing: the Spectre, a chiral aperiodic monotile
(Recorded event from Monday, June 5)
Two months later, the same team (comprised of MoMath’s Outreach Mathematician Chaim Goodman-Strauss, along with co-authors Craig Kaplan, Joseph Myers, and Dave Smith) uncovered “the Spectre” — an aperiodic monotile that is “chiral,” meaning that reflected copies of the tile are not needed to form a tiling and no tiling with unreflected copies has a repeating pattern.  What an exciting breakthrough yet again in mathematics!  Watch the video.

Learn about the Spectre

A Chiral Aperiodic Monotile
By David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss
Read about the “Spectre,” a close relative of the recently discovered “Hat,” an aperiodic monotile that mixes unreflected and reflected tiles in every tiling it admits, leaving open the question of whether a single shape can tile aperiodically using translations and rotations alone — a question that is answered in this exciting discovery of the Spectre, a chiral aperiodic monotile.