Math Monday: Hole New Polyhedra
If you build a number of polyhedral models, and count up their vertices, edges, and faces, you many discover an interesting relationship, especially if you look at sums and differences of these quantities.
| polyhedron | vertices | edges | faces |
|---|---|---|---|
| tetrahedron | 4 | 6 | 4 |
| trigonal bipyramid | 5 | 9 | 6 |
| triangular prism | 6 | 9 | 5 |
| cube | 8 | 12 | 6 |
| octahedron | 6 | 12 | 8 |
| bilunabirotunda | 14 | 26 | 14 |
Can you see a numerical pattern in the above? If you don’t find it, don’t worry — you’re in the company of mathematical greats like Euclid and Descartes (the inventor of what we call “Cartesian” coordinates). On the other other hand, if you noticed that for every one of these polyhedra, the number of vertices minus the number of edges plus the number of faces is always equal to two (a formula often written as V–E+F=2), then congratulations! You’ve matched wits with Leonhard Euler, one of the most prolific mathematicians of all time.
In fact, the more polyhedra you make, the more you might begin to think that this equation holds for every possible polyhedron — that is, until you get to something like this one, that I like to call the “Octahex Ring.” 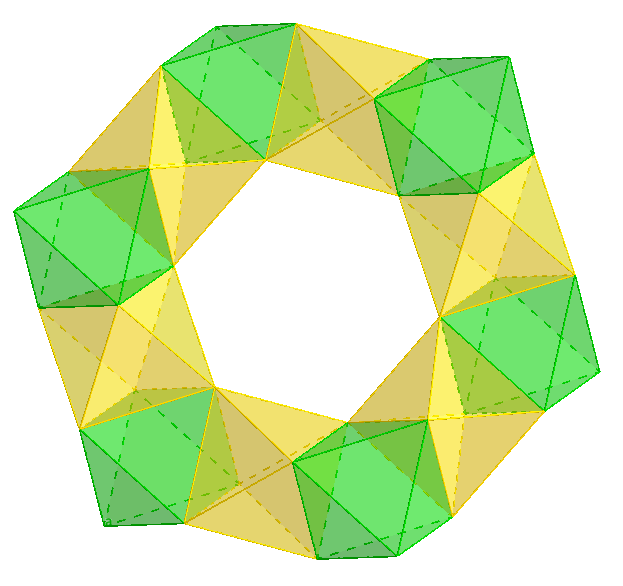
It takes a bit of counting, but if you are careful you can work out that this polyhedron has 36 vertices (every vertex is part of one of the six green units, each of which is an octahedron with six vertices) and 108 edges (six times twelve from the six green units, and six more that are not part of any green unit from each of the six yellow units) and 72 faces (six from each of the twelve units, yellow and green). And doing the arithmetic, 36 – 108 + 72 = 0, not 2. What’s going on?
It turns out that Euler’s formula, V–E+F, is more powerful than it seems at first glance. There’s clearly something a little unusual about the octahex ring: it’s shaped kind of like a doughnut; it has a “hole” going through its middle. And that’s exactly what this simple formula can detect, and even count: for any polyhedron at all, V–E+F tells you the number of holes. If this quantity comes out to 2, there are no holes; if it comes out to 0, there is one hole; -2 means two holes; -4 means three holes; and so on, decreasing by 2 with each additional hole. How such a basic formula based on the elementary parts of the shape can tell you about the complicated overall property of having holes or not is a beautiful story unfortunately too long to tell here, bringing together ideas from many different branches of mathematics.
What does this have to do with making? Thanks to the ParaGons system mentioned in a few recent posts, students in many classrooms have had the opportunity to, and had great success with, building the octahex ring and experiencing its interesting and unusual structure first hand. Math Mondays wants to thank all of the teachers, schools, and students involved, many of whom are pictured below.
Here are Jessica Quinn’s students at Mayfield Senior School in Pasadena starting to assemble the green corner units of the octahex ring. 
And here are Mayra Oliden’s students at Dr. Olga Mohan High School starting to link some units together.

Here’s Cinthia Vega’s 11th grade students at Alhambra High School about to finish up their ring.

And to wrap up, here are photos of the completed efforts of all of these groups, plus an additional group led by teacher Douglas Moroke.







