Math Monday: Bagel Cutting Revisited
DECEMBER 6, 2010
It has now been one year since I started writing these Math Monday columns on MAKE for The Museum of Mathematics. Thinking back to the first column on cutting linked bagel halves, I thought an appropriate anniversary column would show yet another interesting way to cut a bagel. Slicing on a slanted plane which is tangent to the surface at two places reveals a geometric surprise.
The planar cross section is two overlapping circles called Villarceau circles after the French mathematician, Yvon Villarceau, who wrote about them in the mid 1800s.
I’ve indicated them here with colored markers, but you can see they are not perfectly round on a real bagel, because of its flat bottom and other irregularities. On an ideal torus, this slanted slice gives two perfect overlapping circles.
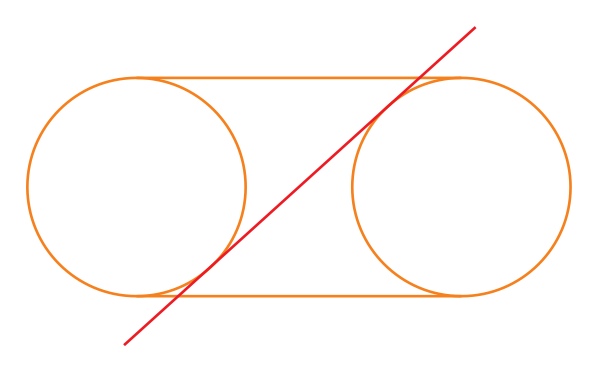
The proper position and slant of the slice will depend on the size of the bagel’s hole. As the above side-view shows, the slicing plane (red) must be chosen so it is tangent to the bagel at two places.
This article first appeared on Make: Online, December 6, 2010.