Math Monday: Tetraxis® Puzzle
JANUARY 25, 2010

People have been making geometric puzzles for centuries, with each design adding new twists. At the Museum of Mathematics, we have a large puzzle called the Tetraxis®, shown above. The name comes from the fact that the pieces line up along four axes. Most people are familiar with the 90 degree relationship between the standard XYZ axes, but are confounded by these parts, which line up in the directions of the four long diagonals of a cube. This puzzle was made by John and Jane Kostick, who incorporated magnets to make the parts lock together nicely. The outer shape is the same as in a family of related puzzles by Stewart Coffin, whose book The Puzzling World of Polyhedral Dissections gives instructions for woodworkers to make their own copies of many geometric puzzles.
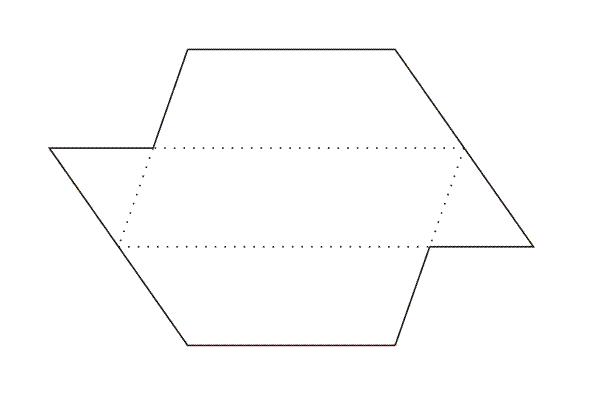
You can make your own paper version by cutting out twelve copies of the above template, folding on the dotted lines, and taping them closed.

Then put the twelve identical parts together to make the form shown at right. Since the paper version has no magnets to hold it together, you may want to tape them to each other. Can you assemble the twelve parts as shown using three rubber bands that hold it together and indicate the XYZ planes? For an extra challenge, make three pieces in each of four colors or four pieces in each of three colors and see what symmetric color patterns you can create.
You can buy a plastic version of this puzzle at the Museum of Mathematics shop.
This article first appeared on Make: Online, January 25, 2010.
Return to Math Monday Archive.